1. SERIES AND PARALLEL LCR CIRCUITS
2.. I-V CHARACTERISTICS OF A ZENER DIODE
3. CHARACTERISTICS OF A TRANSISTOR
4. BAND GAP OF A SEMICONDUCTOR
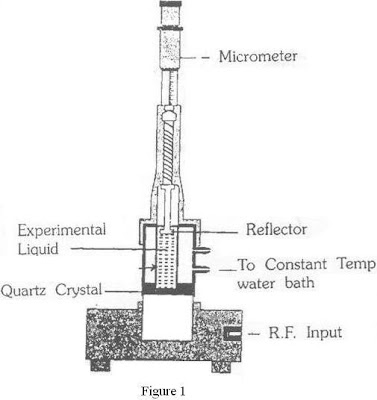
5. ULTRASONIC INTERFEROMETER (MEASUREMENT OF VELOCITY OF SOUND IN SOLIDS AND LIQUIDS)
6. DIELECTRIC CONSTANT (MEASUREMENT OF DIELECTRIC CONSTANT)
7. MAGNETIC PROPERTIES (B-H GRAPH METHOD)
8. DIFFRACTION (MEASUREMENT OF WAVELENGTH OF LASER/Hg SOURCE USING DIFFRACTION GRATING)
9. PLANCK’S CONSTANT (DETERMINATION OF PLANCK’S CONSTANT USING LED OR USING THE PRINCIPLE OF PHOTOELECTRIC EFFECT)
10. ELECTRICAL RESISTIVITY (FOUR PROBE METHOD)
11. VERIFICATION OF STEFAN’S LAW
12. DETERMINATION OF FERMI ENERGY


















.bmp)
.bmp)


